Omarm getallenreeks Fibonacci: je vindt hem overal terug [column]

Het is heel nat geweest. Door de ijzeren poort groeit de Euphorbia, in het Nederlands is de bloem bekend als Wolfsmelk. Ik denk aan de Italiaanse wiskundige Fibonacci, de bijnaam van Leonardo Pisano. Naar Fibonacci is een bekende wiskundige reeks vernoemd. Een serie van getallen waarvan het nieuwe getal telkens verkregen kan worden door de voorgaande twee getallen bij elkaar op te tellen.
Getallenreeksen
Heel kort dan, het begin is als volgt: 0, 1, 1, 2, 3, 5, 8. En het volgende getal krijg je door 5 bij 8 op te tellen, 13 dus, enzovoorts. Nu zou je deze reeks ook kunnen gebruiken om de voortplanting van konijnen uit te leggen. Als konijnen iedere maand jonkies krijgen zodra ze vruchtbaar zijn zal de populatie zich ontwikkelen volgens deze reeks.
Een andere getallenreeks vindt je terug in de wet van Moore, die in 1965 beschrijft dat het aantal transistoren op elektronische circuits ongeveer iedere twee jaar zal verdubbelen (de reeks: 1, 2, 4, 8, et cetera). Hij kreeg gelijk en daarnaast ging deze verdubbeling in capaciteit gepaard met een prijsdaling, zodat we binnenkort met een bril op ons hoofd kunnen gaan lopen, de Google Glass, die slechts zo’n 1500 euro zal kosten. Een weggeefprijs voor wat je allemaal krijgt. We hebben dan een verzameling technologie op ons hoofd waar je in 1965 een volwaardige studio, een aggregaat, een raffinaderij en een watergekoelde mainframe met kubieke meters kelder voor nodig zou hebben. Nu zit alles verpakt in een brillenpoot.
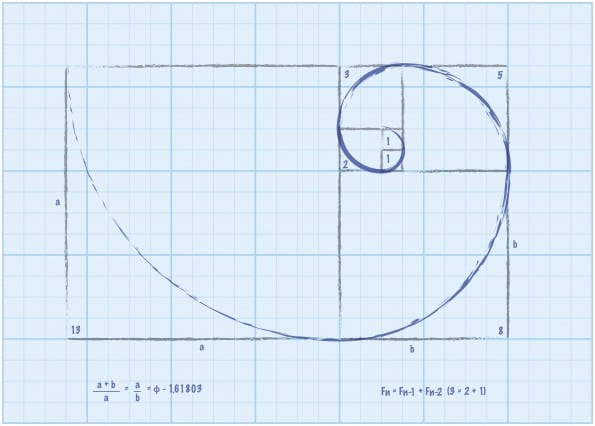
Alles leidt terug naar de reeks van Fibonacci
De Fibonacci-reeks is natuurlijker dan de exponentiële. Je zou Fibonacci kunnen toepassen om het tempo van de groei van een organisatie te beschrijven. Wil je de cultuur bewaren, dan zou de uitbreiding nooit groter mogen zijn dan het tempo van Fibonacci. Meesters hebben tijd nodig om leerlingen op te leiden. Een organisatie van 8 personen zou in een jaar nooit harder mogen groeien dan naar 13 personen, het volgende getal in de reeks. Fibonacci heeft niet alleen met voortplantende konijnen te maken, je vindt het ook op vele plaatsen terug in de kunst. Of in je lichaam, in de verhoudingen van de vingerkoten, de schikking van de zaden van een zonnebloem, de afmetingen van het Parthenon en de piramides van Gizeh, Leonardo da Vinci; het voert allemaal terug naar de reeks van Fibonacci. En deze reeks heeft weer alles te maken met de Gulden Snede. Deel twee opeenvolgende getallen van Fibonacci op elkaar en je krijgt de verhouding van de Gulden Snede.
Overal zie ik opeens Fibonacci en de gulden snede. In de bogen van de Nieuwe Kerk, in het hek en de Wolfsmelk, in de wandelstok van oud premier Piet de Jong, in de stoet op de loper, Beatrix en Mabel (1 en 1), Willem-Alexander en Maxima (2), prinsesjes (3). Dit is een pleidooi voor meer Fibonacci. Vergeet Moore verder, hij heeft zijn werk gedaan, zijn tempo kan de mensheid straks niet meer bijbenen. Omarm Fibonacci.
Deze column werd eveneens gepubliceerd in Het Financieele Dagblad.


 Employee Experience
Employee Experience 





